Linear Model



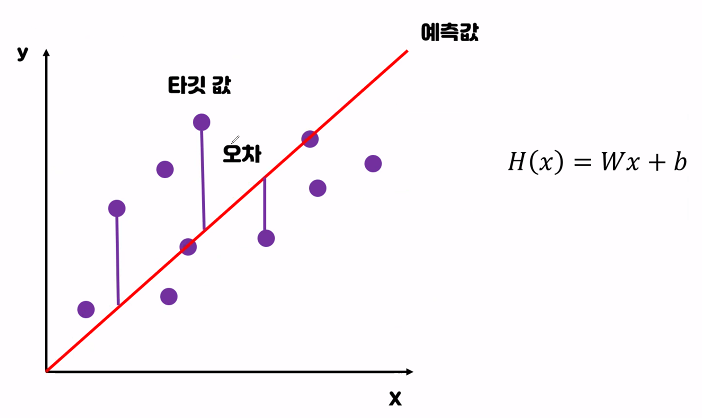
오차:실제 데이터와 모델이
예측한 값의 차이

H(x) : 예측값 y : 실제값
예측값에서 실제값을 뺀 오차를
제곱 후 더하고 데이터 수로 나눈다
2 -2 가 나왔을때 0이 되지않게 하기위해 제곱하는데
절대값이아니라 제곱하는이유:
cost값을 크게 만들어 학습을 빠르게 시키기위해
Linear Model - Regression(Gradient descent algorithm) 경사하강법

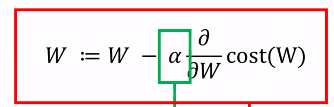
Cost값(기울기)이 가장 낮은 지점을 찾는다

Learning rate가 클때는 크게 움직이며 완벽한 지점을 찾지는 못하고
작을때는 좀 더 정확한 지점을 찾지만 학습시간이 오래걸린다
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
data = pd.DataFrame([[2,20],
[4,40],
[8,80],
[9,90]] , index = ['태양', '민호', '채윤', '연이'],
columns = ['시간','성적'])
data
시간 성적
태양 2 20
민호 4 40
채윤 8 80
연이 9 901. 수학 공식을 이용한 해석적 모델
- LinearRegression
from sklearn.linear_model import LinearRegression
l_model = LinearRegression()
l_model.fit(data[['시간']],data['성적'])
LinearRegression()print(l_model.coef_) # w, 가중치값
print(l_model.intercept_) # b, 절편(편향)값
[10.]
7.105427357601002e-15 # 0에 가깝다2. 경사하강법
- SGDRegressor (Stochastic Gradient Descent)
from sklearn.linear_model import SGDRegressor
sgd_model = SGDRegressor(max_iter=1000, # 가중치 업데이트 반복횟수(epoch)
eta0=0.01, # 학습률(learning rate)
verbose = 1 # 1: 학습과정을 확인할 수 있다.
)
sgd_model.fit(data[['시간']],data['성적'])
-- Epoch 1
Norm: 8.92, NNZs: 1, Bias: 1.101983, T: 4, Avg. loss: 926.737253
Total training time: 0.00 seconds.
-- Epoch 2
Norm: 9.60, NNZs: 1, Bias: 1.199155, T: 8, Avg. loss: 9.937324
Total training time: 0.00 seconds.
-- Epoch 3
Norm: 9.76, NNZs: 1, Bias: 1.214055, T: 12, Avg. loss: 0.899245
Total training time: 0.00 seconds.
-- Epoch 4
Norm: 9.81, NNZs: 1, Bias: 1.217313, T: 16, Avg. loss: 0.234643
Total training time: 0.00 seconds.
-- Epoch 5
Norm: 9.82, NNZs: 1, Bias: 1.213543, T: 20, Avg. loss: 0.163976
Total training time: 0.00 seconds.
-- Epoch 6
Norm: 9.84, NNZs: 1, Bias: 1.210979, T: 24, Avg. loss: 0.157413
Total training time: 0.00 seconds.
-- Epoch 7
Norm: 9.83, NNZs: 1, Bias: 1.206037, T: 28, Avg. loss: 0.152554
Total training time: 0.00 seconds.
..........................................
-- Epoch 37
Norm: 9.85, NNZs: 1, Bias: 1.113796, T: 148, Avg. loss: 0.127976
Total training time: 0.00 seconds.
-- Epoch 48
Norm: 9.85, NNZs: 1, Bias: 1.087605, T: 192, Avg. loss: 0.122182
Total training time: 0.00 seconds.
Norm: 9.85, NNZs: 1, Bias: 1.074026, T: 216, Avg. loss: 0.119024
Total training time: 0.01 seconds.
Convergence after 54 epochs took 0.01 secondsNorm : 가중치, loss : Cost값, Bias : b값.
sgd_model.predict([[7]])
array([70.04650285])print(sgd_model.coef_) # w, 가중치값
print(sgd_model.intercept_) # b, 절편(편향)값
[9.85321092]
[1.07402638]



Lasso 규제는 값을 정하고 가중치에서 규제값을 빼주기 때문에 특정계수가 0이 될 수 있다.
Linear Model - Regression
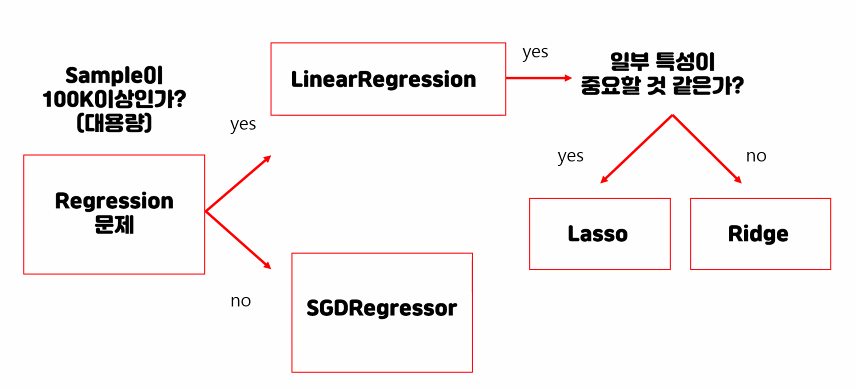
Linear Model - Classification

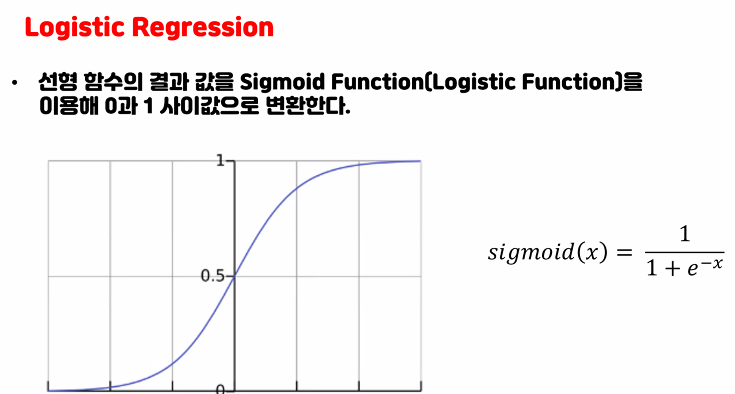
sigmoid식으로 값이 들어가서
다음 식의 결과
0~1사이의 값으로 변환된다.



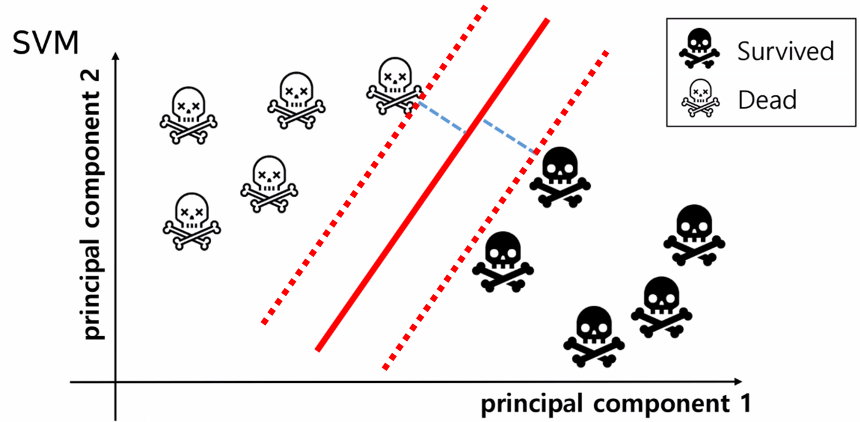
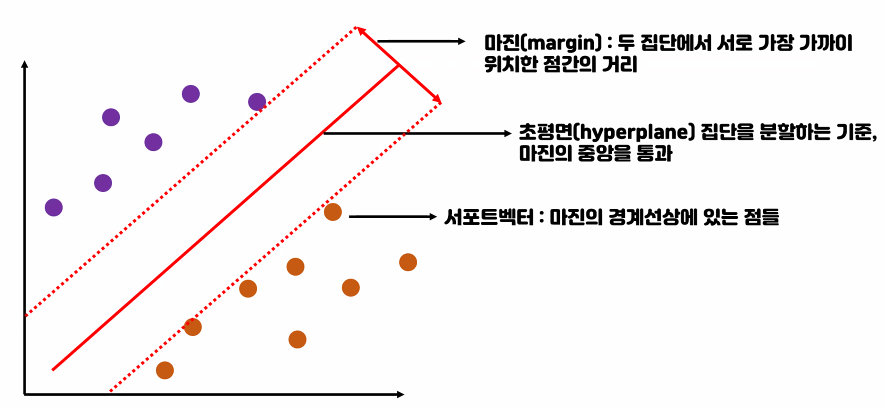
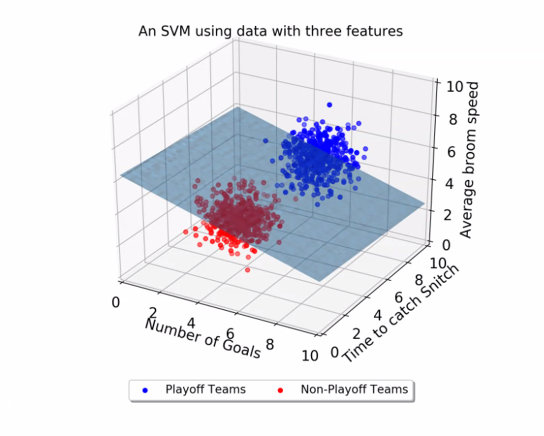
분류시에 나누는 선(예측값)이 데이터들과 떨어져 있는게 좋다

'빅데이터 서비스 교육 > 머신러닝' 카테고리의 다른 글
| 앙상블 모델 (0) | 2022.07.05 |
|---|---|
| Linear Model 실습 (0) | 2022.07.01 |
| 예제 타이타닉 생존자 예측분석 (0) | 2022.06.24 |
| Cross validation (0) | 2022.06.24 |
| 머신러닝 Decision Tree (0) | 2022.06.24 |