보스턴 주택 값 예측 실습
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import load_boston # 보스턴 주택값 데이터
boston = load_boston()
boston_df = pd.DataFrame(boston.data, columns = boston.feature_names)
boston_df.head()
CRIM ZN INDUS CHAS NOX RM AGE DIS RAD TAX PTRATIO B LSTAT
0 0.00632 18.0 2.31 0.0 0.538 6.575 65.2 4.0900 1.0 296.0 15.3 396.90 4.98
1 0.02731 0.0 7.07 0.0 0.469 6.421 78.9 4.9671 2.0 242.0 17.8 396.90 9.14
2 0.02729 0.0 7.07 0.0 0.469 7.185 61.1 4.9671 2.0 242.0 17.8 392.83 4.03
3 0.03237 0.0 2.18 0.0 0.458 6.998 45.8 6.0622 3.0 222.0 18.7 394.63 2.94
4 0.06905 0.0 2.18 0.0 0.458 7.147 54.2 6.0622 3.0 222.0 18.7 396.90 5.33train, test 분리
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(boston_df, boston.target,
test_size =0.3,
random_state=1)
모델적용
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import cross_val_score
l_model = LinearRegression()
l_model.fit(X_train, y_train)
LinearRegression()l_model.score(X_test,y_test)
0.7836295385076281print(l_model.coef_)
print(l_model.intercept_)
[-9.85424717e-02 6.07841138e-02 5.91715401e-02 2.43955988e+00 # 가중치의 개수는
-2.14699650e+01 2.79581385e+00 3.57459778e-03 -1.51627218e+00 # 특성의 수와 같다
3.07541745e-01 -1.12800166e-02 -1.00546640e+00 6.45018446e-03
-5.68834539e-01]
46.396493871823864result=cross_val_score(l_model, X_train,y_train, cv=5)
result.mean()
0.6643081077199126특성확장
e_X_train = X_train.copy()
for i in X_train.columns:
for j in X_train.columns:
e_X_train[i+'x'+j] = X_train[i] * X_train[j]
e_X_train.head()
CRIM ZN INDUS CHAS NOX RM AGE DIS RAD TAX ... LSTATxCHAS LSTATxNOX LSTATxRM LSTATxAGE LSTATxDIS LSTATxRAD LSTATxTAX LSTATxPTRATIO LSTATxB LSTATxLSTAT
13 0.62976 0.0 8.14 0.0 0.538 5.949 61.8 4.7075 4.0 307.0 ... 0.0 4.44388 49.13874 510.468 38.883950 33.04 2535.82 173.460 3278.3940 68.2276
61 0.17171 25.0 5.13 0.0 0.453 5.966 93.4 6.8185 8.0 284.0 ... 0.0 6.54132 86.14904 1348.696 98.459140 115.52 4100.96 284.468 5459.4752 208.5136
377 9.82349 0.0 18.10 0.0 0.671 6.794 98.8 1.3580 24.0 666.0 ... 0.0 14.25204 144.30456 2098.512 28.843920 509.76 14145.84 429.048 8430.1560 451.1376
39 0.02763 75.0 2.95 0.0 0.428 6.595 21.8 5.4011 3.0 252.0 ... 0.0 1.84896 28.49040 94.176 23.332752 12.96 1088.64 79.056 1709.1216 18.6624
365 4.55587 0.0 18.10 0.0 0.718 3.561 87.9 1.6132 24.0 666.0 ... 0.0 5.11216 25.35432 625.848 11.485984 170.88 4741.92 143.824 2525.4640 50.6944
5 rows × 182 columnse_X_train.shape
(354, 182)l_model = LinearRegression()
l_model.fit(e_X_train, y_train)
LinearRegression()e_X_test = X_test.copy()
for i in X_test.columns:
for j in X_test.columns:
e_X_test[i+'x'+j] = X_test[i] * X_test[j]
l_model.score(e_X_test, y_test)
0.8043803930997194
Ridge (L2규제)
from sklearn.linear_model import Ridge
r_model = Ridge() # alpha= 로 규제의 강도 설정
r_model.fit(e_X_train, y_train)
r_model.score(e_X_test,y_test)
0.8239994029608095Ridge vs Lasso
from sklearn.linear_model import Lasso
alpha_list =[0.001, 0.01, 0.1, 10 , 100, 1000]
r_coef = []
l_coef = []
for i in alpha_list:
r_model = Ridge(alpha =i)
l_model = Lasso(alpha =i)
r_model.fit(e_X_train,y_train)
l_model.fit(e_X_train,y_train)
r_coef.append(r_model.coef_)
l_coef.append(l_model.coef_)
len(r_coef)
6
len(l_coef)
6
r_df = pd.DataFrame(np.array(r_coef).T, columns=alpha_list) #.T -> arrayList의 축을 바꿀때 사용
r_df
0.001 0.010 0.100 10.000 100.000 1000.000
0 -2.967946 -3.084029 -2.661836 -0.075861 -0.004695 0.000504
1 0.440672 0.414180 0.314357 -0.194214 -0.158361 -0.035165
2 -4.971540 -4.576505 -3.893822 -0.230469 0.007065 0.004058
3 37.790726 27.202270 7.193797 0.101728 0.005391 0.000041
4 42.723740 6.367370 0.419346 0.029559 0.005779 0.000777
... ... ... ... ... ... ...
177 -0.009413 -0.009255 -0.010853 -0.018205 -0.018827 -0.015527
178 -0.000908 -0.000899 -0.000819 0.000001 0.000127 -0.000010
179 0.019950 0.020062 0.021877 0.016719 0.012587 0.005452
180 -0.000297 -0.000308 -0.000322 -0.000315 -0.000292 -0.000085
181 0.015527 0.015380 0.015380 0.020819 0.025236 0.031515
182 rows × 6 columnsdef plot(coef, alpha):
plt.figure(figsize = (20,5))
plt.bar(e_X_train.columns, coef)
plt.title('alpha ={}'.format(alpha))
plt.ylim([-13,5])
plt.show()
cnt = 0
for i in alpha_list:
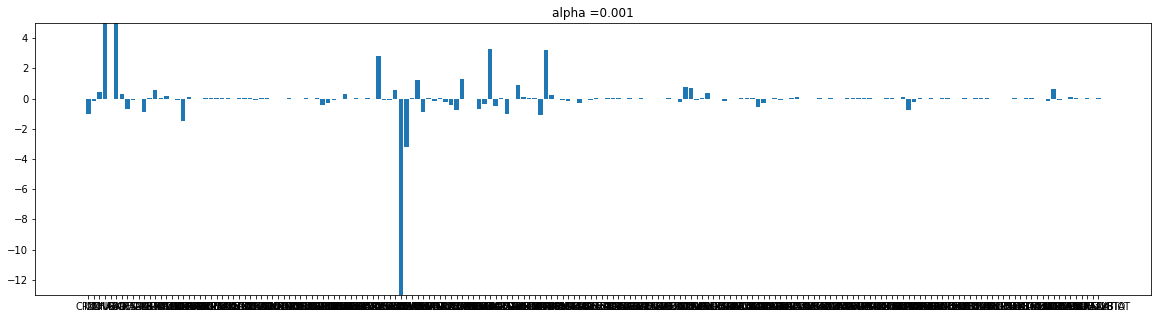
plot(r_coef[cnt], i)
cnt+=1
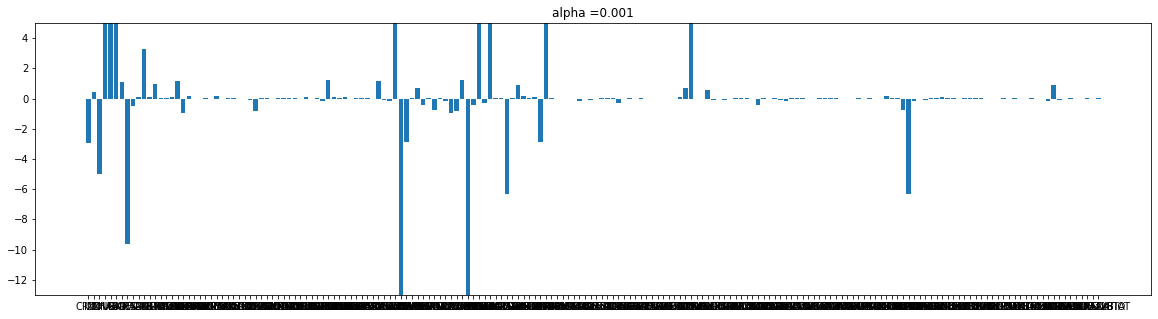
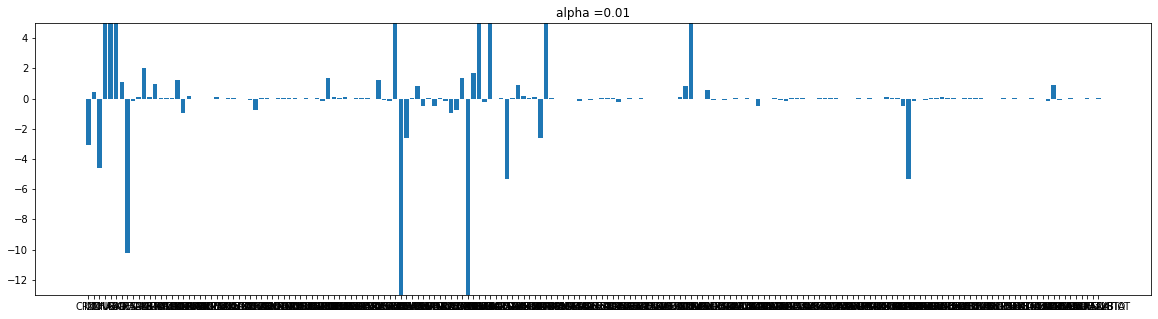
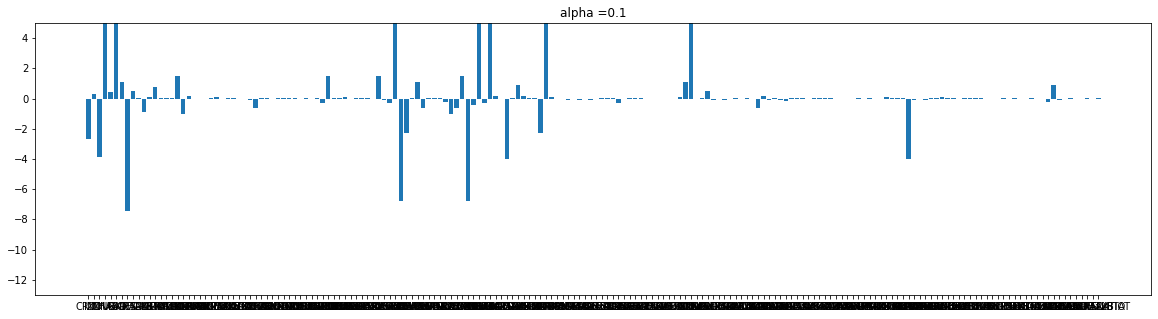
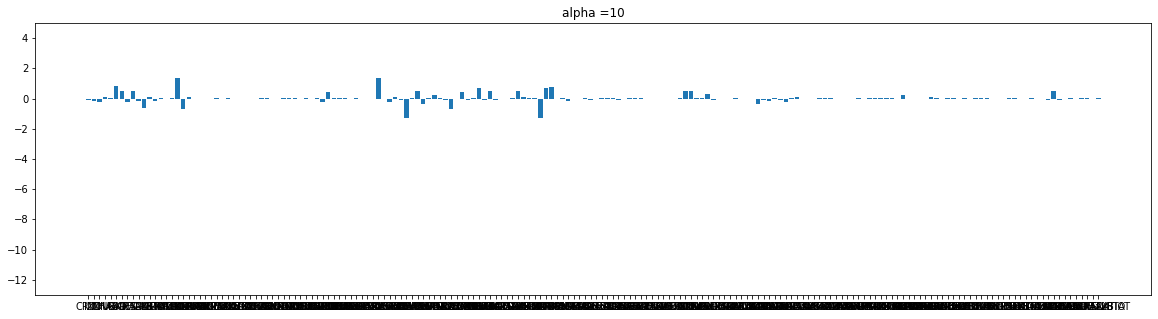


Ridge는 규제가 강해질수록 가중치가 작아진다.
cnt = 0
for i in alpha_list:
plot(l_coef[cnt], i)
cnt+=1
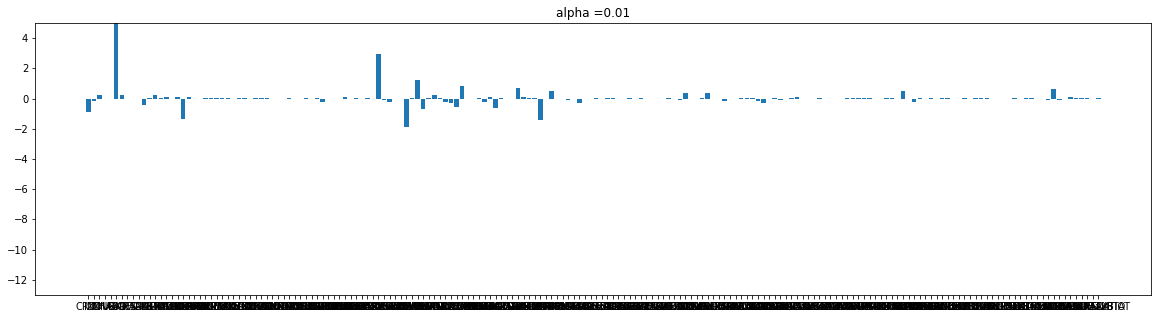
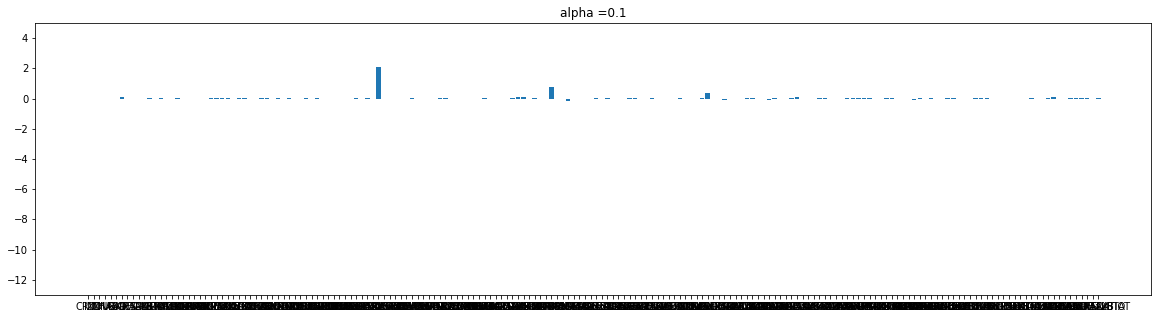



Lasso는 규제가 강해 질수록 가중치가 사라진다
손글씨 분류 실습
목표
- 손 글씨 숫자(0~9)를 분류하는 모델을 만들어 보자.
- 이미지 데이터의 형태를 이해
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
data = pd.read_csv('./data/digit_train.csv')
data.head()
label pixel0 pixel1 pixel2 pixel3 pixel4 pixel5 pixel6 pixel7 pixel8 ... pixel774 pixel775 pixel776 pixel777 pixel778 pixel779 pixel780 pixel781 pixel782 pixel783
0 1 0 0 0 0 0 0 0 0 0 ... 0 0 0 0 0 0 0 0 0 0
1 0 0 0 0 0 0 0 0 0 0 ... 0 0 0 0 0 0 0 0 0 0
2 1 0 0 0 0 0 0 0 0 0 ... 0 0 0 0 0 0 0 0 0 0
3 4 0 0 0 0 0 0 0 0 0 ... 0 0 0 0 0 0 0 0 0 0
4 0 0 0 0 0 0 0 0 0 0 ... 0 0 0 0 0 0 0 0 0 0
5 rows × 785 columnsdata.shape
(42000, 785)img0 = data.iloc[0,1:]
print(img0.max())
print(img0.min())
255
0img0.values.reshape(28,28) # imshow 안에는 이미지를 넣어야 하므로
# 1차원인 img0을 2차원형태(28X28)로 reshape한다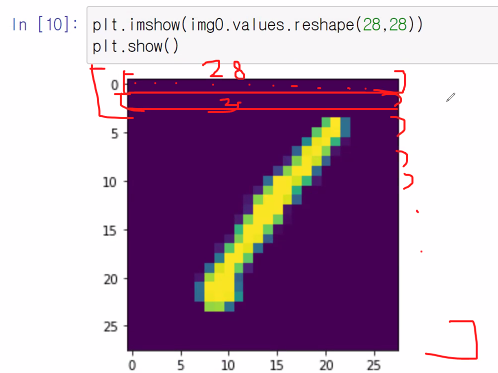
28개의 데이터 28줄
img1 = data.iloc[1,1:]
plt.imshow(img1.values.reshape(28,28), cmap='gray')

5000장 추출
X = data.iloc[:5000,1:]
y = data.iloc[:5000,0]
print(X.shape)
print(y.shape)(5000, 784)
(5000,)from sklearn.model_selection import train_test_split
X_train, X_test, y_train,y_test = train_test_split(X,y,test_size=0.3, random_state=1)
모델설계
- KNN
- Decision tree
- Logisitc regression
- SVM
from sklearn.neighbors import KNeighborsClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.svm import LinearSVC
knn = KNeighborsClassifier()
tree = DecisionTreeClassifier()
logi = LogisticRegression()
svm = LinearSVC()
knn.fit(X_train,y_train)
tree.fit(X_train,y_train)
logi.fit(X_train,y_train)
svm.fit(X_train,y_train)
print('knn : ',knn.score(X_test,y_test))
print('tree : ',tree.score(X_test,y_test))
print('logi : ',logi.score(X_test,y_test))
print('svm : ',svm.score(X_test,y_test))knn : 0.914
tree : 0.7426666666666667
logi : 0.872
svm : 0.812스케일링
from sklearn.preprocessing import MinMaxScaler
Mms = MinMaxScaler()
Mms.fit(X_train)
X_train_s = Mms.transform(X_train)
X_test_s = Mms.transform(X_test)
knn.fit(X_train_s,y_train)
tree.fit(X_train_s,y_train)
logi.fit(X_train_s,y_train)
svm.fit(X_train_s,y_train)
print('knn : ',knn.score(X_test_s,y_test))
print('tree : ',tree.score(X_test_s,y_test))
print('logi : ',logi.score(X_test_s,y_test))
print('svm : ',svm.score(X_test_s,y_test))knn : 0.914
tree : 0.746
logi : 0.882
svm : 0.8433333333333334예측
img5 = X_test_s[5]
knn.predict([img5]) # img5는 1차원 -> [img5]로 2차원으로 만들어준다(fit했을때와 동일한형태로)
array([9], dtype=int64)y_test[5] #답이 예측과 다른값
0array([[0. , 0. , 0. , 0. , 0. , 0. , 1. , 0. , 0. , 0. ],
[0. , 1. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. ],
[0. , 0. , 0. , 0. , 0.2, 0. , 0. , 0.8, 0. , 0. ],
[0. , 0. , 0. , 0. , 0. , 1. , 0. , 0. , 0. , 0. ],
[0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 1. , 0. ],
[0. , 0. , 1. , 0. , 0. , 0. , 0. , 0. , 0. , 0. ],
[0. , 1. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. ],
[0. , 0. , 1. , 0. , 0. , 0. , 0. , 0. , 0. , 0. ],
[0. , 0.4, 0.6, 0. , 0. , 0. , 0. , 0. , 0. , 0. ],
[0. , 0. , 1. , 0. , 0. , 0. , 0. , 0. , 0. , 0. ],
[1. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. ],
[1. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. ],
[0. , 0. , 0. , 0. , 0. , 0. , 0. , 1. , 0. , 0. ],
[0. , 0. , 0. , 0. , 0. , 1. , 0. , 0. , 0. , 0. ],
[0. , 0. , 0. , 0.2, 0. , 0.2, 0. , 0. , 0.6, 0. ],
[0. , 0. , 0. , 0. , 0. , 0. , 1. , 0. , 0. , 0. ],
[1. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. ],
[1. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. ],
[0. , 0. , 0. , 0. , 1. , 0. , 0. , 0. , 0. , 0. ],
[0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 1. , 0. ]])순서대로 1 2 3 4 5 6 7 8 9 일 확률을 예측한다 -> 그래서 가장 높은 확률인 숫자를 예측값으로 반환한다.
분류평가지표
from sklearn.metrics import classification_report
pre = knn.predict(X_test_s)
print(classification_report(pre,y_test))
print(classification_report(pre,y_test))
print(classification_report(pre,y_test))
precision recall f1-score support
0 0.98 0.93 0.95 165
1 0.99 0.83 0.90 172
2 0.85 0.97 0.91 155
3 0.91 0.91 0.91 149
4 0.92 0.95 0.93 136
5 0.93 0.90 0.91 146
6 0.97 0.94 0.95 156
7 0.90 0.92 0.91 151
8 0.78 0.97 0.87 120
9 0.91 0.86 0.89 150
accuracy 0.91 1500
macro avg 0.92 0.92 0.91 1500
weighted avg 0.92 0.91 0.91 1500
# f1-score : 재현율, 정밀도 둘다 고려한 수치
분류평가지표
오차행렬
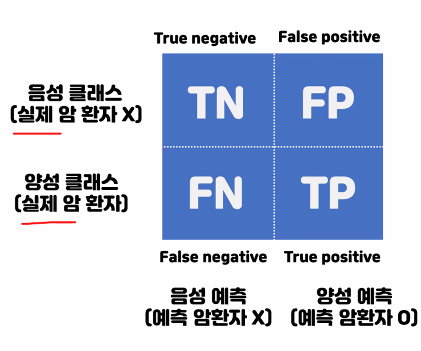
Y축 클래스 : 답
X축 예측 : 예측값
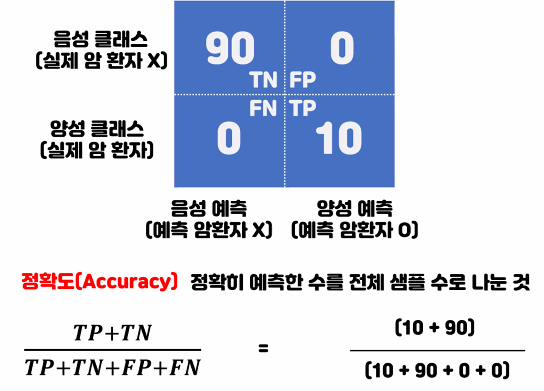
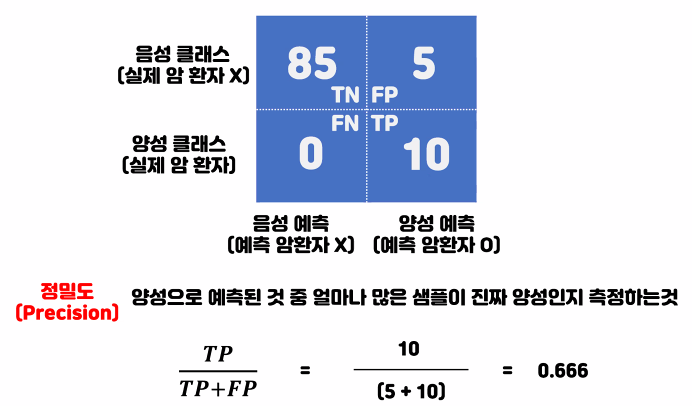
정밀도
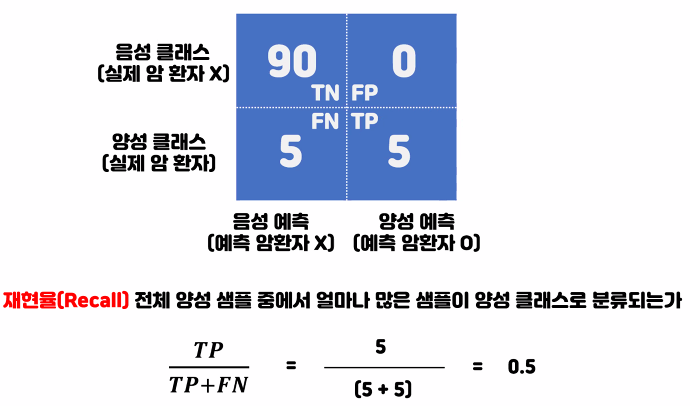
재현율

예측 결과가 잘못되었을때 큰 위험이 있을때(실제 상황에대한 리스크가 클때) -> 높은 재현율이 필요
모델이 예측 할때 비용이 많이 들때(모델에 대한 리스크[ex 비용이클때]가 클때) -> 높은 정밀도 필요
'빅데이터 서비스 교육 > 머신러닝' 카테고리의 다른 글
| 텍스트 마이닝 (0) | 2022.07.06 |
|---|---|
| 앙상블 모델 (0) | 2022.07.05 |
| Linear Model (0) | 2022.06.29 |
| 예제 타이타닉 생존자 예측분석 (0) | 2022.06.24 |
| Cross validation (0) | 2022.06.24 |